2002年全国高中数学联赛试题
(第一试) |
一、 选择题(本题满分36分,每小题6分)
1、函数f(x)=log1/2(x2-2x-3)的单调递增区间是( )。
(A)(-∞,-1) (B)(-∞,1) (C)(1,+∞) (D)(3,+∞)
2、若实数x,y满足(x+5)2+(y-12)2=142,则x2+y2的最小值为( )。
(A)2 (B)1 (C)√3 (D)√2
3、函数f(x)=x/(1-2x)-x/2( )
(A)是偶函数但不是奇函数(B)是奇函数但不是偶函数(C)既是偶函数又是奇函数(D)既不是偶函数也不是奇函数
4、直线x/4+y/3=1与椭圆x2/16+y2/9=1相交于A,B两点,该椭圆上点P,使得ΔPAB面积等于3,这样的点P共有( )。
(A)1个 (B)2个 (C)3个 (D)4个
5、已知两个实数集合A={a1,a2,…,a100}与B={b1,b2,…,b50},若从A到B的映射f使得B中每个元素都有原象,且f(a1)≤f(a2)≤…≤f(a100)则这样的映射共有( )。
(A)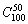 (B) (B)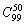 (C) (C)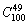 (D) (D)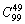 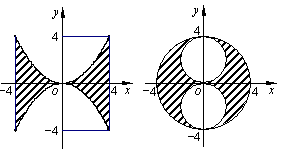
6、由曲线x2=4y,x2=-4y,x=4,x=-4围成的图形绕y轴旋转一周所得旋转体的体积为V1;满足x2+y2≤16,x2+(y-2)2≥4,x2+(y+2)2≥4的点(x,y)组成的图形绕y轴旋转一周所得旋转体的体积为V2,则( )。
(A)V1=(1/2)V2 (B)V1=(2/3)V2
(C)V1=V2 (D)V1=2V2
二、填空题(本题满分54分,每小题9分)
7、已知复数Z1,Z2满足∣Z1∣=2,∣Z2∣=3,若它们所对应向量的夹角为60°,则∣(Z1+Z2)/(Z1+Z2)∣= 。
8、将二项式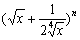 的展开式按x的降幂排列,若前三项系数成等差数列,则该展开式中x的幂指数是整数的项共有 个。 的展开式按x的降幂排列,若前三项系数成等差数列,则该展开式中x的幂指数是整数的项共有 个。
9、如图,点P1,P2,…,P 10分别是四面体顶点或棱的中点,那么在同一平面上的四点组(P1,Pi,Pj,Pk)(1<i<j<k≤10)有 个。
10、已知f(x)是定义在R上的函数,f(1)=1且对任意x∈R都有f(x+5)≥f(x)+5,f(x+1)≤f(x)+1。若g(x)=f(x)+1-x,则g(2002)= 。
11、若log4(x+2y)+log4(x-2y)=1,则∣x∣-∣y∣的最小值是 。
12、使不等式sin2x+acosx+a2≥1+cosx对一切x∈R恒成立的负数a的取值范围是 。
三、解答题(本题满分60分,每小题20分)
13、已知点A(0,2)和抛物线y2=x+4上两点B,C使得AB⊥BC,求点C的纵坐标的取值范围。
14、如图,有一列曲线P0,P1,P2……,已知P0所围成的图形是面积为1的等边三角形,Pk+1是对Pk进行如下操作得到:将Pk的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(k=0,1,2,)。记Sn为曲线Pn所围成图形的面积。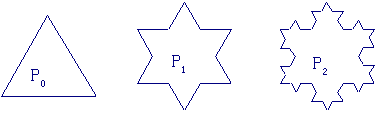 …… ……
(1)求数列{Sn}的通项公式;
(2)求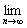 Sn. Sn.
15、设二次函数f(x)=ax2+bx+c(a,b,c∈R,a≠0)满足条件:
(1)当x∈R时,f(x-4)=f(2-x),且f(x)≥x;
(2)当x∈(0,2)时,f(x)≤((x+1)/2)2;
(3)f(x)在R上的最小值为0.
求最大的m(m>1),使得存在t∈R,只要x∈[1,m],就有f(x+t)≤x。
|
2002年全国高中数学联赛试题
(第二试) |
|
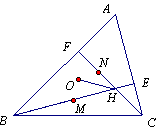 一.(本题满分50分) 一.(本题满分50分)
如图,在△ABC中,∠A=60°, AB>AC, 点O是外心,两条高BE、CF交于H点。
点M、N分别在线段BH、HF上,且满足BM=CN 。
求:(MH + NH)/OH 的值 。
二.(本题满分50分)
实数a,b,c和正数 λ 使得 f(x)=x3+ax2+bx+c 有三个实根x1,x2,x3, 且满足
(1)x2 - x1=λ
(2)x3 >(x1+x2)/2
求:(2a3 + 27c - 9ab)/λ3 的最大值 。
三.(本题满分50分)
在世界杯足球赛前,F国教练为了考察A1,A2,…,A7这七名队员,准备让他们在三场训练比赛(每场90分钟)都上场。假设在比赛的任何时刻,这些队员中有且仅有一人在场上,并且A1,A2,A3,A4每人上场的总时间(以分钟为单位)均被7整除,A5,A6,A7每人上场的总时间(以分钟为单位)均被13整除.如果每场换人次数不限,那么按每名队员上场的总时间计算,共有多少种不同的情况。
| |
















