|
|
 |
专题栏目 |
 |
 |
相关文章 |
 |
|
|
|
|
 |
[组图]2001年全国高中数学联合竞赛试题 |
热 ★★★ |
|
2001年全国高中数学联合竞赛试题
|
|
作者:佚名 文章来源:本站原创 点击数: 更新时间:2005/8/15 10:11:35  |
|
2001年全国高中数学联赛试题
第 1 试 |
一、 选择题(本题满分36分,每小题6分)
1.已知a为给定的实数,那么集合M={x|x2-3x-a2+2=0,x∈R}的子集的个数为( )
(A)1 (B)2 (C)4 (D)不确定
2.命题1 长方体中,必存在到各顶点距离相等的点;
命题2 长方体中,必存在到各棱距离相等的点;
命题3 长方体中,必存在到各面距离相等的点。
以上三个命题中正确的有 ( )
(A)0个 (B)1个 (C)2个 (D) 3个
3. 在四个函数y=sin|x|, y=cos|x|, y=|ctgx|, y=lg|sinx|中以π为周期,在(0,π/2)上单调递增的偶函数是( )
(A)y=sin|x| (B)y=cos|x| (C)y=|ctgx| (D)y=lg|sinx|
4. 如果满足∠ABC=60°, AC=12, BC=k的△ABC恰有一个, 那么k的取值范围是( )
(A)k=8√3 (B)0<k≤12 (C)k≥12 (D)0<k≤12或k=8√3
5. 若(1+x+x2)1000的展开式为a0+a1x+a2x2+…a2000x2000,则a0+a3+a6+a9+…+a1998的值为( )
(A)3333 (B)3666 (C)3999 (D)32001
6. 已知6枝玫瑰与3枝康乃馨的价格之和大于24元,而4枝玫瑰与5枝康乃馨的价格之和小于22元,则2枝玫瑰的价格和3枝康乃馨的价格比较结果是 ( )
(A)2枝玫瑰的价格高 (B)3枝康乃馨的价格高 (C)价格相同 (D)不确定
二、填空题(本题满分54分,每小题9分)
7. 椭圆ρ=1/(2-cosθ)的短轴长等于________.
8.若复数z1,z2满足|z1|=2,|z2|=3,3z1-2z2=3/2-i,则z1·z2=_________.
9.正方体ABCD-A1B1C1D1的棱长为1,则直线A1C1与BD1的距离是________.
10.不等式|1/log1/2x+2|>3/2的解集为__________________.
11.函数y=x+√(x2-3x+2)的值域为______________. 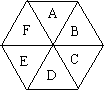
12.在一个正六边形的六个区域栽种观赏植物(如图),要求同一块中种同一种植物,相邻的两块种不同的植物。现有4种不同的植物可供选择,则有________种栽种方案。
三、解答题(本题满分60分,每小题20分)
13.设{an}为等差数列,{bn}为等比数列,且b1=a12, b2=a22, b3=a32(a1<a2), 又(b1+b2+…+bn)的极限=√2+1。 试求{an}的首项和公差。[注意:√2+1和√(2+1)表示的数字不相同]
14.设曲线C1:x2/a2+y2=1(a为正常数)与C2:y2=2(x+m)在x轴上方仅有一个公共点P。
(1)求实数m的取值范围(用a表示); (2)O为原点,若C1与x轴的负半轴交于点A,当0<a<1/2时,试求△OAP的面积的最大值(用a表示)。
15.用电阻值分别为a1、a2、a3、a4、a5、a6的电阻组成一个如图的组件,在组装的过程中如何选择电阻,才能使该组件的电阻值最小?证明你的结论。
 |
2001年全国高中数学联赛试题
第 2 试 |
|
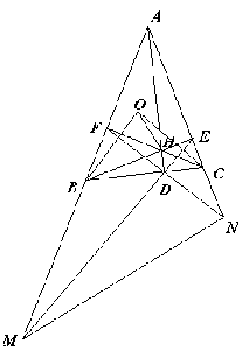 一.(本题满分50分) 一.(本题满分50分)
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N 。
求证:(1) OB⊥DF,OC⊥DE
(2) OH⊥MN。
二、(本题满分50分)
设 xi ≥ 0 ,i∈N+ ,且 ∑1≤i≤n(xi2) + ∑1≤k≤j≤n( √(k/j)×xkxj ) = 1 。
求:∑1≤i≤n xi 的最小值 。
三.(本题满分50分)
将边长为正整数m,n的矩形划分成若干边长均为正整数的正方形.每个正方形的边均平行于矩形的相应边.试求这些正方形边长之和的最小值.
| |
|
| 数学竞赛录入:admin 责任编辑:admin |
|
|
上一个数学竞赛: 2000年全国高中数学联合竞赛试题
下一个数学竞赛: 2002年全国高中数学联合竞赛试题 |
|
|
| 【字体:小 大】【发表评论】【加入收藏】【告诉好友】【打印此文】【关闭窗口】 |
|
 网友评论:(只显示最新10条。评论内容只代表网友观点,与本站立场无关!) 网友评论:(只显示最新10条。评论内容只代表网友观点,与本站立场无关!) |
| |
|
|
|
|
















