|
|
 |
专题栏目 |
 |
 |
相关文章 |
 |
|
|
|
|
 |
[图文]1999年全国高中数学联合竞赛试题 |
热 ★★★ |
|
1999年全国高中数学联合竞赛试题
|
|
作者:佚名 文章来源:本站原创 点击数: 更新时间:2005/8/15 10:06:00  |
|
1999年全国高中数学联合竞赛试题
第一试 |
| 一. 选择题(满分36分,每小题6分) |
1. 给定公比为q(q≠1)的等比数列{an},设b1=a1+a2+a3,b2=a4+a5+a6,…,bn=a3n-2+a3n-1+a3n,…,则数列{bn}( )
(A)是等差数列 (B)是公比为q的等比数列 (C)是公比为q3的等比数列 (D)既非等差数列也非等比数列
2. 平面直角坐标系中,纵、横坐标都是整数的点叫做整点,那么,满足不等式 (|x|-1)2+(|y|-1)2<2的整点(x,y)的个数是( )
(A)16 (B)17 (C)18 (D)25
3. 若(log23)x - (log53)x ≥ (log23)-y - (log53)-y,则( )
(A)x-y≥0 (B)x+y≥0 (C)x-y≤0 (D)x+y≤0
4. 给定下列两个关于异面直线的命题:
命题Ⅰ:若平面a上的直线a与平面b上的直线b为异面直线,直线c是a与b的交线,那么c至多与a,b中的一条相交;
命题Ⅱ:不存在这样的无穷多条直线,它们中的任意两条都是异面直线。
那么,( )
(A)命题Ⅰ正确,命题Ⅱ不正确 (B)命题Ⅱ正确,命题Ⅰ不正确 (C)两个命题都正确 (D)两个命题都不正确
5. 在某次乒乓球单打比赛中,原计划每两名选手恰比赛一场,但有3名选手各比赛了2场之后就退出了,这样,全部比赛只进行了50场。那么,在上述3名选手之间比赛的场数是( )
(A)0 (B)1 (C)2 (D)3
6. 已知点A(1,2),过点(5,-2)的直线与抛物线y2=4x交于另外两点B,C,那么,△ABC是( )
(A)锐角三角形 (B)钝角三角形 (C)直角三角形 (D)答案不确定 |
| 二. 填空题(满分54分,每小题9分) |
1. 已知正整数n不超过2000,并且能表示成不少于60个连续正整数之和,那么,这样的n的个数是___________.
2. 已知θ=arctg(5/12),那么复数z=(cos2θ+isin2θ)/(239+i)的辐角主值是__________.
3. 在△ABC中,记BC=a,CA=b,AB=c,若9a2+9b2-19c2=0,则ctgC/(ctgA+ctgB)=__________.
4. 已知点P在双曲线x2/16-y2/9上,并且P到这条双曲线的右准线的距离恰是P到这条双曲线的两个焦点的距离的等差中项,那么,P的横坐标是_____.
5. 已知直线ax+by+c=0中的a,b,c是取自集合{-3,-2,-1,0,1,2,,3}中的3个不同的元素,并且该直线的倾斜角为锐角,那么,这样的直线的条数是_______.
6. 已知三棱锥S-ABC的底面是正三角形,A点在侧面SBC上的射影H是△SBC的垂心,二面角H-AB-C的平面角等于30°, SA=2√3。那么三棱锥S-ABC的体积为__________.[注:√表示根号] |
| 三、(满分20分)已知当x∈[0,1]时,不等式x2cosθ-x(1-x)+(1-x)2sinθ > 0恒成立,试求θ的取值范围. |
| 四、(满分20分)给定A(-2,2),已知B是椭圆上的动点,F是左焦点,当|AB|+5|BF|/3取最小值时,求B的坐标. |
| 五、(满分20分)给定正整数n和正数M,对于满足条件a12 + an+12≤M的所有等差数列a1,a2,a3,…,试求S=an+1 + an+2 + … +a2n+1的最大值. |
1999年全国高中数学联合竞赛试题
第二试 |
|
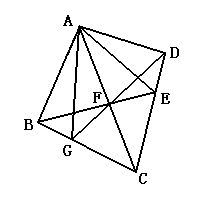 一、(本题满分50分) 一、(本题满分50分)
如图,在四边形ABCD中,对角线AC平分∠BAD,在CD上取一点E,BE与AC相交于F,延长DF交BC于G。求证:∠GAC=∠EAC。
二、(本题满分50分)
给定实数a,b,c,已知复数 z1,z2,z3 满足:|z1| = |z2| = |z3| = 1 ,z1/z2 = z2/z3 = z3/z1,求 |az1+bz2+cz3| 的值。
三、(本题满分50分)
给定正整数 n,己知用克数都是正整数的 k 块砝码和一台天平可以称出质量为1,2,3,…,n克的所有物品。
(1)求 k 的最小值 f(n);
(2)当且仅当 n 取什么值时,上述 f(n) 块砝码的组成方式是唯一确定的?并证明你的结论。 | |
|
| 数学竞赛录入:admin 责任编辑:admin |
|
|
上一个数学竞赛: 1998年全国高中数学联合竞赛试题
下一个数学竞赛: 2000年全国高中数学联合竞赛试题 |
|
|
| 【字体:小 大】【发表评论】【加入收藏】【告诉好友】【打印此文】【关闭窗口】 |
|
 网友评论:(只显示最新10条。评论内容只代表网友观点,与本站立场无关!) 网友评论:(只显示最新10条。评论内容只代表网友观点,与本站立场无关!) |
| |
|
|
|
|
















