一九九八年全国高中数学联合竞赛试卷
第一试 |
| 一、选择题(本题满分36分,每小题6分) |
1.若a>1,b>1且lg(a+b)=lga+lgb,则lg(a-1)+lg(b-1)的值 ( )
(A) 等于lg2 (B)等于1 (C)等于0 (D)不是与a,b无关的常数
2.若非空集合A={x|2a+1≤x≤3a-5},B={x|3≤x≤22},则能使A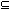 A∩B成立的所有a的集合是( ) A∩B成立的所有a的集合是( )
(A){a|1≤a≤9} (B){a|6≤a≤9} (C){a|a≤9} (D)空集
3.各项均为实数的等比数列{an}前n项和记为Sn,若S10=10,S30=70,则S40等于( )
(A) 150 (B) -200 (C) 150或-200 (D)400或-50
4.设命题P:关于x的不等式a1x2+b1x+c1>0与a2x2+b2x+c2>0的解集相同;命题Q:a1/a2=b1/b2=c1/c2。则命题 Q ( )
(A)是命题P的充分必要条件 (B)是命题P的充分条件但不是必要条件
(C)是命题P的必要条件但不是充分条件 (D)既不是命题P的充分条件也不是命题P的必要条件 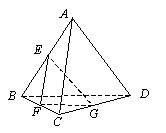
5.设E ,F,G分别是正四面体ABCD的棱AB,BC,CD的中点,则二面角C-FG-E的大小是( )
(A)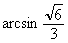 (B) (B) 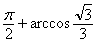
(C)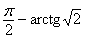 (D) (D)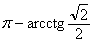
6.在正方体的8个顶点,12条棱的中点,6个面的中心及正方体的中心共27个点中,共线的三点组的个数是( )
(A) 57 (B) 49 (C) 43 (D) 37 |
| 二、填空题(本题满分54分,每小题9分) |
1.若f(x) (x∈R)是以2为周期的偶函数,当x∈[0,1]时,f(x)=x(1/1998),则f(98/19),f(101/17),f(104/15)由小到大的排列是_________________.
2.设复数z=cosθ+isinθ(0°≤θ≤180°),复数z,(1+i)z,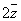 在复平面上对应的三个点分别是P,Q,R,当P,Q,R不共线时,以线段PQ,PR为两边的平行四边形的第四个顶点为S,则点S到原点距离的最大值是_______. 在复平面上对应的三个点分别是P,Q,R,当P,Q,R不共线时,以线段PQ,PR为两边的平行四边形的第四个顶点为S,则点S到原点距离的最大值是_______.
3.从0,1,2,3,4,5,6,7,8,9这10个数中取出3个数,使其和为不小于10的偶数,不同的取法有________种. 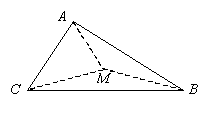
4.各项为实数的等差数列的公差为4,其首项的平方与其余各项之和不超过100,这样的数列至多有___________项.
5.若椭圆x2+4(y-a)2=4与抛物线x2=2y有公共点,则实数a的取值范围是_____________.
6.△ABC中,∠C=90°,∠B=30°,AC=2,M是AB的中点,将△ACM沿CM折起,使A,B两点间的距离为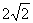 ,此时三棱锥A-BCM的体积等于________. ,此时三棱锥A-BCM的体积等于________. |
三、(本题满分20分)已知复数z=1-sinθ+icos(θ) (π/2 < θ < π),求z的共轭复数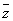 的辐角主值。 的辐角主值。 |
四、(本题满分20分)设函数f(x)=ax2+8x+3(a<0),对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f (x)|≤5都成立。
问:a为何值时l(a)最大?求出这个最大的l(a),证明你的结论。 |
五、(本题满分20分) 已知抛物线y2=2px及定点A(a,b),B(-a,0),(ab≠0,b2≠2pa),M是抛物线上的点,设直线AM,BM与抛物线的另一交点分别为M1,M2.
求证:当M点在抛物线上变动时(只要M1,M2存在且M1≠M2),直线M1M2恒过一个定点,并求出这个定点的坐标。 |
| |
一九九八年全国高中数学联合竞赛试卷
第二试 |
|
一、(50分)如图,O、I 分别为ΔABC的外心和内心,AD是BC边上的高,I在线段OD上。求证:ΔABC的外接圆半径等于BC边上的
旁切圆半径。
注:ΔAB 的BC边上的旁切圆是与边AB、AC的延长线以及边BC都相切的圆。
二、(50分)设 a1,a2, … ,an ;b1,b2, … ,bn∈[ 1,2 ] 且 a12 + a22 + … + an2 = b12 + b22 + … + bn2。
设 Xi = ai3/bi 求证:X1 + X2 + … + Xn ≤ 17( a12 + a22 + … + an2 )/10。并问:等号成立的充要条件。
三、对于正整数 a、n ,定义 Fn(a)= q + r ,其中 q、r 为非负整数,a = qn + r ,且 0≤ r < n 。求最大的正整数A,使得存在正整数 n_1 ,n_2 ,n_3 , n_4 ,n_5 ,n_6 ,对于任意的正整数 a ≤A ,都有
Fn_6(Fn_5(Fn_4(Fn_3(Fn_2(Fn_1(a))))))= 1
证明你的结论。
| | |
















