|
|
 |
专题栏目 |
 |
 |
相关文章 |
 |
|
|
|
|
 |
[组图]1995年全国高中数学联合竞赛试题 |
热 ★★★ |
|
1995年全国高中数学联合竞赛试题
|
|
作者:佚名 文章来源:本站原创 点击数: 更新时间:2005/8/15 9:47:37  |
|
1995年全国高中数学联赛试题
( 第 一 试 ) |
| 一.选择题(每小题6分,共36分) |
1. 设等差数列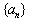 满足 满足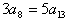 且 且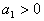 ,Sn为其前项之和,则Sn中最大的是( ) ,Sn为其前项之和,则Sn中最大的是( )
(A) (B) (B)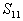 (C) (C)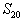 (D) (D)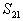
2. 设复平面上单位圆内接正20边形的20个顶点所对应的复数依次为 Z1,Z2,…Z20,则复数Z11995,Z21995,…Z201995所对应的不同的点的个数是( )
(A)4 (B)5 (C)10 (D)20
3. 如果甲的身高数或体重数至少有一项比乙大,则称甲不亚于乙,在100个小伙子中,如果某人不亚于其他99人,就称他为棒小伙子,那么,100个小伙子中的棒小伙子最多可能有( )
(A)1个 B)2个 (C)50个 (D)100个
4. 已知方程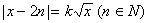 在区间(2n-1,2n+1]上有两个不相等的实根,则k的取值范围是( ) 在区间(2n-1,2n+1]上有两个不相等的实根,则k的取值范围是( )
(A)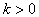 (B) (B)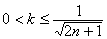 (C) (C)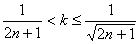 (D)以上都不是 (D)以上都不是
5. logsin1cos1,logsin1tg1,logcos1sin1,logcos1tg1的大小关系是( )
(A) logsin1cos1<logcos1sin1<logsin1tg1<logcos1tg1
(B) logcos1sin1<logcos1tg1<logsin1cos1<logsin1tg1
(C) logsin1tg1<logcos1tg1<logcos1sin1<logsin1cos1
(D) logcos1tg1<logsin1tg1<logsin1cos1<logcos1sin1
6. 设O是正三棱锥P-ABC底面三角形ABC的中心,过O的动平面与PC交于S,与PA,PB的延长线分别交于Q,R,则和式1/PQ+1/PR+1/PS ( )
(A)有最大值而无最小值 (B)有最小值而无最大值
(C)既有最大值又有最小值,两者不等 (D)是一个与面QPS无关的常数 |
| 二、填空题(每小题9分,共54分) |
1. 设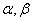 为一对共轭复数,若 为一对共轭复数,若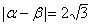 ,且 ,且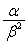 为实数,则 为实数,则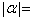 _____. _____.
2. 一个球的内接圆锥的最大体积与这个球的体积之比为_______.
3. 用[x]表示不大于实数x的最大整数, 方程lg2x + [lg x] - 2 = 0的实根个数是______.
4. 直角坐标平面上,满足不等式组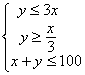 的整点个数是______. 的整点个数是______.
5. 将一个四棱锥的每个顶点染上一种颜色,并使同一条棱的两端点异色,如果只有5种颜色可使用,那么不同的染色方法的总数是______.
6. 设M={1,2,3,…,1995},A是M的子集且满足条件:当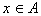 时, 时,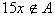 ,则A中元素的个数最多是______ . ,则A中元素的个数最多是______ . |
1995年全国高中数学联赛试题
( 第二试 ) |
 一、(25分) 给定曲线族 2(2sinθ-cosθ+3)x2 - (8sinθ+cosθ+1)y = 0,θ为参数,求该曲线在直线 y=2x 上所截得的弦长的最大值. 一、(25分) 给定曲线族 2(2sinθ-cosθ+3)x2 - (8sinθ+cosθ+1)y = 0,θ为参数,求该曲线在直线 y=2x 上所截得的弦长的最大值.
二、(25分) 求一切实数p,使得三次方程5x^3-5(p+1)x^2+(71p-1)x+1=66p的三个根均为自然数.
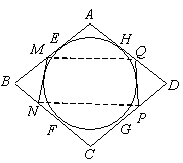
三、(35分) 如图,菱形ABCD的内切圆O与各边分别切于E,F,G,H,在弧EF与GH上分别作圆O的切线交AB于M,交BC于N,交CD于P,交DA于Q,求证: MQ//NP.
四、(35分) 将平面上的每个点都以红,蓝两色之一着色。证明:存在这样两个相似的三角形,它们的相似比为1995,并且每一个三角形的三个顶点同色. | |
|
| 数学竞赛录入:admin 责任编辑:admin |
|
|
上一个数学竞赛: 1994年全国高中数学联合竞赛试题
下一个数学竞赛: 1996年全国高中数学联合竞赛试题 |
|
|
| 【字体:小 大】【发表评论】【加入收藏】【告诉好友】【打印此文】【关闭窗口】 |
|
 网友评论:(只显示最新10条。评论内容只代表网友观点,与本站立场无关!) 网友评论:(只显示最新10条。评论内容只代表网友观点,与本站立场无关!) |
| |
|
|
|
|
















