1993年全国高中数学联合竞赛试卷
第 一 试 |
| 一.选择题(每小题5分,共30分) |
1. 若M={(x,y)| |tgpy|+sin2px=0},N={(x,y)| x2+y2≤2},则 M∩N 的元素个数是( )
(A)4 (B)5 (C)8 (D)9
2. 已知f(x)=asinx+b+4(a,b为实数),且 f(lglog310)=5,则f(lglg3)的值是( )
(A)-5 (B)-3 (C)3 (D)随a,b取不同值而取不同值
3. 集合A,B的并集 A∪B ={a1,a2,a3},当A≠B时,(A,B)与(B,A)视为不同的对,则这样的(A,B)对的个数是( )
(A)8 (B)9 (C)26 (D)27
4. 若直线x=π/4 被曲线C:(x-arcsina)(x-arccosa)+(y-arcsina)(y+arccosa)=0所截的弦长为d,当a变化时d的最小值是( )
(A)π/4 (B) π/3 (C)π/2 (D)π
5. 在△ABC中,角A,B,C的对边长分别为a,b,c,若c-a等于AC边上的高h,则sin((C-A)/2)+cos((C+A)/2)的值是( )
(A)1 (B)1/2 (C)1/3 (D)-1
6.设m,n为非零复数,i为虚数单位,z∈C,则方程| z+ni|+| z-mi|=n与| z+ni|-|z-mi|=-m在同一复平面内的图形(F1,F2为焦点)是( )

|
| 二.填空题(每小题5分,共30分) |
1. 二次方程(1-i)x2+(λ+i)x+(1+iλ)=0(i为虚数单位,λ∈R)有两个虚根的充分必要条件是λ的取值范围为________.
2. 实数x,y满足4x2-5xy+4y2=5,设 S=x2+y2,则_______.
3. 若z∈C,arg(z2-4)=5π/6,arg(z2+4)=π/3,则z的值是________.
4. 整数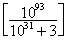 的末两位数是_______. (注:[a]表示不大于a的最大整数) 的末两位数是_______. (注:[a]表示不大于a的最大整数)
5. 设任意实数x0>x1>x2>x3>0,要使log(x0/x1)1993+log(x1/x2)1993+log(x2/x3)1993≥klog(x0/x3)1993恒成立,则k的最大值是_______.
6. 三位数(100,101,…,999)共900个,在卡片上打印这些三位数,每张卡片上打印一个三位数,有的卡片所印的,倒过来看仍为三位数,如198倒过来看是861;有的卡片则不然,如531倒过来看是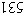 ,因此,有些卡片可以一卡二用,于是至多可以少打印_____张卡片. ,因此,有些卡片可以一卡二用,于是至多可以少打印_____张卡片. |
三.(本题满分20分)
三棱锥S-ABC中,侧棱SA、SB、SC两两互相垂直,M为三角形ABC的重心,D为AB的中点,作与SC平行的直线DP.证明:(1)DP与SM相交;(2)设DP与SM的交点为D',则D'为三棱锥S-ABC的外接球球心. |
四.(本题满分20分)
设0<a<b,过两定点A(a,0)和B(b,0)分别引直线l和m,使与抛物线y2=x有四个不同的交点,当这四点共圆时,求这种直线l与m的交点P的轨迹. |
|
五.(本题满分20分)
设正数列a0,a1,a2,…,an,…满足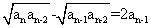 (n≥2)且a0=a1=1.求{an}的通项公式. (n≥2)且a0=a1=1.求{an}的通项公式. |
1993年全国高中数学联合竞赛试卷
第 二 试 |
一.(35分) 设一凸四边形ABCD,它的内角中仅有∠D是钝角,用一些直线段将该凸四边形分割成n个钝角三角形,但除去A、B、C、D外,在该四边形的周界上,不含分割出的钝角三角形顶点.试证n应满足的充分必要条件是n≥4.
二.(35分) 设A是一个有n个元素的集合,A的m个子集A1,A2,…,Am两两互不包含. 试证:
(1)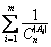 ≤1; (2) ≤1; (2)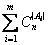 ≥m2. ≥m2.
其中|Ai|表示Ai所含元素的个数,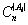 表示n个不同元素取|Ai|个的组合数. 表示n个不同元素取|Ai|个的组合数.
三.(35分) 水平直线m通过圆O的中心,直线 l⊥m,l与m相交于M,点M在圆心的右侧,直线l上不同的三点A,B,C在圆外,且位于直线m上方,A点离M点最远,C点离M点最近,AP,BQ,CR为圆O的三条切线,P,Q,R为切点.试证:
(1)l与圆O相切时,AB×CR+BC×AP=AC×BQ;
(2)l与圆O相交时,AB×CR+BC×AP<AC×BQ;
(3)l与圆O相离时,AB×CR+BC×AP>AC×BQ. | |
















