|
|
 |
专题栏目 |
 |
 |
相关文章 |
 |
|
|
|
|
 |
[组图]1992年全国高中数学联合竞赛试题 |
热 ★★★ |
|
1992年全国高中数学联合竞赛试题
|
|
作者:佚名 文章来源:本站原创 点击数: 更新时间:2005/8/15 9:04:59  |
|
1992年全国高中数学联赛试卷
第一试 |
| 一.选择题(每小题5分,共30分) |
1. 对于每个自然数n,抛物线y=(n2+n)x2-(2n+1)x+1与x轴交于An,Bn两点,以|AnBn|表示该两点的距离,则|A1B1|+|A2B2|+…+|A1992B1992|的值是( )
(A)1991/1992 (B)1992/1993 (C)1991/1993 (D)1993/1992
2. 已知如图的曲线是以原点为圆心,1为半径的圆的一部分,则这一曲线的方程是( )
(A)(x+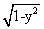 )(y+ )(y+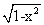 )=0 (B)(x- )=0 (B)(x-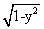 )(y- )(y-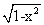 )=0 )=0
(C)(x+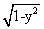 )(y- )(y-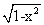 )=0 (D)(x- )=0 (D)(x-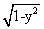 )(y+ )(y+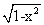 )=0 )=0
3. 设四面体四个面的面积分别为S1,S2,S3,S4,它们的最大值为S,记λ=(S1+S2+S3+S4)/S,则λ一定满足( )
(A)2<λ≤4 (B)3<λ<4 (C)2.5<λ≤4.5 (D)3.5<λ<5.5
4. 在△ABC中,角A,B,C的对边分别记为a,b,c(b≠1),且C/A,sinB/sinA都是方程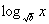 =logb(4x-4)的根,则△ABC( ) =logb(4x-4)的根,则△ABC( )
(A)是等腰三角形,但不是直角三角形 (B)是直角三角形,但不是等腰三角形
(C)是等腰直角三角形 (D)不是等腰三角形,也不是直角三角形
5. 设复数z1,z2在复平面上对应的点分别为A,B,且|z1|=4,4z12-2z1z2+z22=0,0为坐标原点,则△OAB的面积为( )
(A)8√3 (B)4√3 (C)6√3 (D)1√3
[注:√表示根号。另外数字0(零)和字母O(欧)可能会在您的电脑显示器上显示成相同的字符。]
6. 设f(x)是定义在实数集R上的函数,且满足下列关系f(10+x)=f(10-x), f(20-x)=-f(20+x),则f(x)是( )
(A)偶函数,又是周期函数 (B)偶函数,但不是周期函数 (C)奇函数,又是周期函数 (D)奇函数,但不是周期函数 |
| 二.填空题(每小题5分共30分) |
1. 设x,y,z是实数,3x,4y,5z成等比数列,且1/x,1/y,1/z成等差数列,则x/z+z/x的值是______.
2. 在区间[0,π]中,三角方程cos7x=cos5x的解的个数是______.
3. 从正方体的棱和各个面上的对角线中选出k条,使得其中任意两条线段所在的直线都是异面直线,则k的最大值是_____.
4. 设z1,z2都是复数,且|z1|=3,|z2|=5,|z1+z2|=7,则arg(z2/z1)3的值是______.
5. 设数列a1,a2,…,an,…满足a1=a2=1,a3=2,且对任何自然数n, 都有anan+1an+2≠1,又anan+1an+2an+3=an+an+1+an+2+an+3,则a1+a2+…+a100的值是_____.
6. 函数f(x)=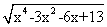 - -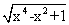 的最大值是_____. 的最大值是_____. |
三、(20分)求证: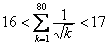 . . |
| 四、(20分)设l,m是两条异面直线,在l上有A,B,C三点,且AB=BC,过A,B,C分别作m的垂线AD,BE,CF,垂足依次是D,E,F,已知AD=√15,BE=7/2,CF=√10,求l与m的距离.[注:√表示根号] |
五、(20分)设n是自然数,fn(x)=(xn+1-x-n-1)/(x-x-1) (x≠0,1,-1),令y=x+(1/x).
1.求证:fn+1(x)=yfn(x)-fn-1(x),(n>1)
2.用数学归纳法证明:
fn(x)=  |
1992年全国高中数学联赛试卷
第二试 |
一、(35分)设A1A2A3A4为⊙O的内接四边形,H1,H2,H3,H4依次为△A2A3A4,△A1A3A4,△A1A2A4,△A1A2A3的垂心,求证:H1,H2,H3,H4四点在同一个圆上,并定出该圆的圆心位置.
二、(35分)设集合 Sn={1,2,…,n}.若X是Sn的子集,把X中所有数的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为的奇(偶)子集.
1.求证 Sn 的奇子集与偶子集个数相等.
2.求证:当 n≥3 时,Sn 的所有奇子集的容量之和等于所有偶子集的容量之和.
3.当 n≥3 时,求 Sn 的所有奇子集的容量之和.
三、(35分)在平面直角坐标系中,横坐标和纵坐标都是整数的点称为格点,任取6个格点Pi (xi,yi)(i=1,2,3,4,5,6)满足
(1) | xi |≤2,| yi |≤2,(i=1,2,3,4,5,6),
(2) 任何三点不在同一条直线上.
试证:在以Pi (i=1,2,3,4,5,6)为顶点的所有三角形中,必有一个三角形,它的面积不大于2. | |
|
| 数学竞赛录入:admin 责任编辑:admin |
|
|
上一个数学竞赛: 没有了
下一个数学竞赛: 1993年全国高中数学联合竞赛试题 |
|
|
| 【字体:小 大】【发表评论】【加入收藏】【告诉好友】【打印此文】【关闭窗口】 |
|
 网友评论:(只显示最新10条。评论内容只代表网友观点,与本站立场无关!) 网友评论:(只显示最新10条。评论内容只代表网友观点,与本站立场无关!) |
| |
|
|
|
|
















