随着著名的发明问题解决理论TRIZ理论的出现，这个想法终于变成可能。

　　TRIZ理论解决创新性问题的思路在于它采用科学的问题求解方法，具体办法就是将特殊的问题归结为TRIZ的一般性问题，然后应用TRIZ带有普遍性的创新理论和算法寻求标准解法，在此基础上演绎形成初始问题的具体解法。这种从特殊到一般的方法，充分体现了科学的问题解决思想，富有可操作性，为计算机环境下的创新工作提供了重要的理论与方法基础。

　　实现创新就是要解决前人没有解决的问题或者矛盾。为了更好的应用这些原理解决具体的矛盾，TRIZ理论包含了著名的矛盾矩阵。矛盾矩阵的行和列分别是在大量专利分析基础上总结出来的39个通用技术参数，用这39个通用技术参数中的两个分别表示矛盾体中的两个方面，也就是使系统性能改善的参数和导致系统性能恶化的参数，那么在矩阵中这两个技术参数所在行列的交叉点就对应着实践证明最为有效的创新原理，基于这些创新原理的启发我们就可以寻求具体解决的方案。

　　我们通过一个实例看一下是如何应用创新原理解决实际问题，实现创新的。生活中我们常用扳手拧紧或者松卸螺栓，这时经常会出现螺栓棱角被磨损的问题。为了方便地拧紧或者松动螺栓，又不损坏螺栓，我们采取的方法一般是通过减小扳手卡口和螺栓的配合间隙，增加螺栓的受力面，来减少对棱角的磨损。但结果是提升了制造精度，提高了制造成本。要解决这样一对矛盾，可以用39个技术参数中的两个来描述该矛盾。通过矛盾矩阵我们就可以找到对应的创新原理，如增加不对称性，空间维数变化等。那么应用其中的空间维数变化原理，我们就会有这样一个解决方案：在扳手卡口内壁开几个小弧。因为经过分析我们知道，扳手之所以会磨损螺栓，就是因为作用力都集中在棱角上，是作用在一条线上，现在经过增加几个小弧，使作用力加到螺栓的棱面上，有效地解决了棱角磨损问题(图1)。这项技术已经成为美国的一项专利(图2)，美国的METRINCH公司基于这项技术开发出一系列扳手，获得了巨大利润。

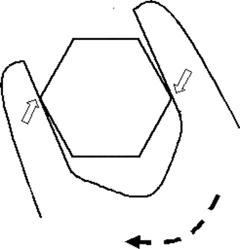
图1.改进前的扳手

图2.改进后的扳手

　　通过上面的例子可以看出，经过深入分析，螺栓被扳手磨损的问题被定义为TRIZ理论中的典型矛盾，结果应用创新原理使得问题得到有效的解决，就像求解数学题一样，整个解决过程变得有序和可操作，大大提高了创新问题的解决效率和质量。