古代希腊包括巴尔干半岛的南部,爱琴海和爱奥尼亚海的岛屿,还有克里特岛和小亚细亚的沿岸地区。半岛的东岸弯拐曲折,海湾很多,风平浪微,有许多优良的港口。
古希腊人非常喜欢旅行和出海贸易,这使他们很早就接触了先进的东方文化。那时候,奴隶担负日常劳动,奴隶主就有足够的时间去评论市政、争辩法律诉讼和海外新闻,以此作为时髦的消遣。于是,那些善辩的人经常把一些人聚集在自己的周围作为门徒。
公元前五百多年,毕达哥拉斯建立了青年兄弟会,以秘密的形式向会员传授数学知识。一个世纪后,雅典出现了学校,给青年讲授法律、政治、演说和数学方面的知识。新式的学校里没有了那种神秘的色彩,不论教师和学生,什么都可以写出来给人看。这种公开研究,自由争论,促进了一种新的数学思想和方法的产生。
很早以前,人们就知道了边长为3、4、5和5、12、13的三角形为直角三角形。毕达哥拉斯发现了这两套数字的共同之处:最大数的平方等于另外两个数的平方和,即3?+4?=5?;5?+12?=13?。这就是说,以直角三角形最长边为边长的正方形面积,等于两个短边为边长的两个正方形面积的和。
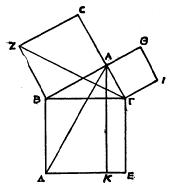
接着,毕达哥拉斯又研究了这样两个问题:一、这个规律是否对所有的直角三角形都成立?二、符合这一规律的任何三角形是否一定是直角三角形?
毕达哥拉斯搜集了许许多多的例子,都肯定回答了这两个问题。据说,他为了庆祝自己的这个发现,曾杀了一百多头牛,举行了一次大宴会。这就是几何学中的勾股定理为什么又叫做毕达哥拉斯定理的由来。
希腊的数学教师同时也讲授法律。学生学习数学也象学习法律那样,对教师给出的每一条法则都提出自己的异议,并且要求教师对所有的概念都作出准确的定义。这样就使得教师面临非常艰巨的任务,尤其是下定义,可不是一件容易的事。比如,怎样确切地定义一条直线?怎样给出圆的定义?怎样使别人不会把它们理解成别的图形?……
不知经过了多少次的争论,人们才逐步意识到,最好的办法就是直截了当地叙述怎样用工具做出图形的。要用工具画图,这又引出了一个问题:什么工具是大家都同意使用的呢?那时的希腊人画几何图形规定只准用画线的直尺和画圆的圆规。
在希腊之前的漫长年代里,人们已经知道了许多求面积和测角度的知识。可是谁也没有想到过用推理的方法把这些知识联系在一起,找出它们之间的内在关系,并且证明它们是可靠的。这就是说,这时的几何知识还处于零散的、互不联系的状态之中。没有系统,就没有几何学。
好辩的希腊人,坚持每一个几何定律都必须通过辩论的验证,并且对各种相反的意见一一做出答复。这样,在证明新的定律时,就可以直接引用已经证明过的定律,而无需一切都从头开始。细心的希腊人对几何知识从不轻信,他们破格相信的只是那些十分清楚的解释和概念。他们从指导思想和具体方法两个方面,推动了几何学的形成和发展。
大约在公元前三百年,欧几里得写了一套叫做《几何原本》的数学教科书,把希腊人在这方面的成就传给了我们。一千年后,许多希腊著作都散失和毁掉了,而《几何原本》却被译成阿拉伯文,作为穆斯林大学的教本。直到五十年前,欧洲和美洲各国的学校还在用翻译的《几何原本》作教科书。就是今天,初中学校里讲授几何学的主要内容也是来自欧几里得几何学。
几何学的建立为测量、建筑、航海、天文,甚至为城市规划、乐器设计等提供了必要的工具。
在毕达哥拉斯时代,希腊人知道的几何法则中有这么两条:一、任何三角形的三个内角和等于两个直角;二、三角形的两个内角相等,它们的对应边也相等。由第一个法则可以得到:如果三角形中有一个角是直角,另一个角是45°,那么第三个角也一定是45°;由第二个法则可以得到:对应于两个45°角的边一定相等。他们根据这两条法则,就可以利用阳光测量出地面上的物体高度了。
当阳光成45°照射地面时,一根直立在地面上的柱子,连同它的影子和阳光,恰好组成这样一个三角形,测量柱高就不用爬到柱子上去了。因为柱子和它的影子都对应着45°的角,二者是等长的,只要量出影长就行了。
当然,这个原理在其它许多方面也用得着。例如,要在岸上测出海上的船只离岸多远,只要在岸上确定两个点,使一个点与船的联线和海岸成直角,另一个点与船的联线与海岸成45°角,那么岸上两点间的距离,就是船与海岸的距离。
这种方法,由于有45°角的要求,在实际测量中受到很大的限制。古埃及人在测量金字塔的高度时,使用了三角形的另一个法则:任意两个三角形,如果对应角相等,那么各组对应边的边长的比也相等。这样,直立在地面上的木杆高度,与它正午影子的长度比,就和金字塔的高度,与它正午影长加上地基宽度一半的比相等。木杆的高度和影长,金字塔的影长和地基的宽度都可以直接量出来。所以,金字塔的高度根据比例关系就能算出来了。
掌握了对应三角形的法则后,角度限制没有了,一年四季里不管什么时候,都可以利用阳光来测量高度了。需要指出的是,古埃及人虽然会使用这个法则,却不会象希腊人那样能严格地证明它。
公元前332年,古希腊的亚历山大大帝征服了埃及,下令在那里建造了亚历山大城。后来,这个城成了地中海的学术中心。
大约在公元前240年,亚历山大城的教师伊拉托瑟尼算出了地球子午线的长度,这是几何知识在历史上的一次重大应用。
伊拉托瑟尼从资料中得知阿斯旺附近的西恩正好在北回归线上。因为夏至那天的中午,在那里的深井里能看到太阳的倒影。这表明太阳正好在头顶的正上方,阳光垂直地面,直射向地球的中心。同是夏至这一天中午,他测量了亚历山大城的一根柱子的影子,算出了阳光偏离垂直方向7.2°。因为阳光是平行直射地面的,所以入射角度的这种差异应该是说明了地球表面的弯曲情况。
现在我们来看看伊拉托瑟尼是怎样运用几何知识算出地球子午线的长度的。如图,画两条平行线:一条表示亚历山大城的太阳光线;另一条表示西恩的太阳光线。画亚历山大城的垂直线—柱子,它切割当地的光线成7.2°;切割西恩的光线于地球中心。
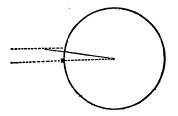
根据平行线的内错角相等的知识,伊拉托瑟尼知道:亚历山大城、地心、西恩间的角度也是7.2°;而7.2°正好是360°圆的1/50。
因为西恩在亚历山大城的正南,所以两地间的道路大体上就在跨越南北极的大圆上。这样,伊拉托瑟尼根据西恩到亚历山大城是480英里,就算出了地球大圆的周长等于480英里的50倍,得到24000英里(相当于38623公里),这就是地球子午线的长度了。我们知道,现在测得的地球子午线的长度是40008.5公里,伊拉托瑟尼的误差还不到4%。在麦哲伦首次环球航行前一千七百多年,就给出了如此精确的近似值,这确实是惊人的成绩!
和伊拉托瑟尼大体同时的阿基米得是那个时代最卓越的数学家、物理学家和机械发明家。他制造了石弩和弩炮来打击敌人,保卫自己的国家。他做出了紧贴圆筒内壁的旋转器来抽水,解决了农田灌溉和船舱排水的困难。著名的浮力原理,也是他在判断皇冠是纯金还是金银混合物时发现的。今天我们用来测量液体密度的比重计,就是依据这个原理做成的。
阿基米得在数学上有许多贡献。他运用圆内接和外切正四十八边形周长的平均数,相当精确地算出了圆周率的值是22/7。直到今天,这个数值足够一般工程技术采用。他研究过曲线的特性,象熏蚊子的盘香那样的曲线,我们今天就把它叫做阿基米得螺线。他还发现了许多求体积的方法。其中两种球和圆柱体的求积方法,就刻在他的墓碑上。
比阿基米得晚五十年的希帕卡斯,汇集了希腊几何学的成就,编制了我们现在说的正弦表,这对测量和天文学极为有用。
我们知道,三角形的三个内角和等于两直角。如果三角形中有一个角为直角,一个为已知角A,那第三个角B就等于直角与角A的差。角A的对边与斜边的比,称为角A的正弦。这个比,对于包括同样角度A的所有直角三角形来说都是一样的。当A为60°、45°、30°时,由勾股定理就可以确定出正弦值。希帕卡斯发现了另外的定理,可以算出其它许多角度的正弦值来,给天文和测量人员提供了很宽的角度范围。
以亚历山大城为科学文化中心长达七百年之久,这是一个繁荣科学技术的时代。城市大规模的建筑,频繁的海上贸易,海陆大国之间连绵不断的战争,促进了测量和制图、航海和天文、采矿和力学的研究。希腊在数学方面的巨大成就,是不断取得科学技术进步的必不可少的条件。
英语中的“算术”一词来源于希腊语。但是希腊语的“算术”并不是今天的数字计算的意思,而很可能是指“数字游戏”。
那时候最著名的是所谓三角数字1、3、6、10等等。它们是按1、1+2、1+2+3、1+2+3+4等等组成的。毕达哥拉斯青年兄弟会发誓保守秘密之一,就是如何说出这组数中的任意一个是多少。
其实,要说出其中任一数是多少的办法很简单。比如要求第五个数,就用(5+1)去乘5,然后被2除,结果得15;要求第二十个数,就用(20+1)去乘20,然后被2除,结果得210。
石子游戏可能是使希腊人找到求连续奇数和的方法的起源。从1开始,连续10个奇数的和是10×10=100;要是增加到20个奇数,那和为20×20=400。
另一种数字游戏可以用芝诺的一个著名诡辩来代表。芝诺是一个很有才能的数学家。他问道:阿溪里斯是古希腊传说中善跑的神,要是让他和乌龟赛跑,并假定他的速度为乌龟的10倍。乌龟先出发了100米。然后,阿溪里斯开始追赶乌龟。当阿溪里斯跑完这100米时,乌龟又已经向前走了10米;当阿溪里斯跑完这10米时,乌龟又向前走了1米……。阿溪里斯的速度再快,走过一段距离总得有一段时间,而在这段时间里,乌龟速度再慢,也总要走出一段距离来。这样说起来,阿溪里斯是永远追不上乌龟了。
人们从实际经验中知道,结果肯定不会是这样的。阿溪里斯一定会超过乌龟的,但是在很长的时间里,人们不知道问题出在了哪里,当然也就不知道怎样才能驳倒芝诺的诡辩了。
今天,我们都可以算出芝诺这个诡辩站不住脚。乌龟尽管可以100米、10米、1米、0.1米、0.01米……赶在阿溪里斯的前面;但是,这总是在离开起点1/9公里之内,不会超过这个范围。所以,阿溪里斯在离开起点1/9公里的地方,就超过了乌龟。在这里,“永远”并没有迷住我们的眼睛。越来越小的许多分数相加,不管小到何等程度,它们的总和有一个具体限度,在数学上就叫做极限。在这里,1/9公里是乌龟在前的极限,所以阿溪里斯一定能超过它。
字母的使用,曾经使希腊人大大简化了文字。他们也希望在数字计算中,能得到同样的便利。最初,希腊人用表示一个数的字头来代表数,这就是用Δ表示10,H代表100,X表示1000,就好像英语中用T代表Ten,H代表Hundred一样。数字再大,就按需要重复这些符号就行了。这种数的写法和埃及的非常象。你看这两种写法,写同一个数3420的样子如图:
到公元五世纪,希腊人采用了一种完全不同的记数方法。他们以头九个字母表示1到9;接着的九个字母表示10到90;最后的九个字母表示100到900;在任何数的前面划一道,表示这个数是原数的一千倍。这个新的数字系统需要27个字母,但是希腊的字母只有24个,所以增加了三个古老的和外来的字母。
采用这种记数方法,唯一的好处是一些大数字简短好写,不占篇幅;严重的毛病是计算困难,使用很不方便。今天,我们在数学中是把字母作为一种简写符号使用的。比如bh/2表示三角形的面积等于底乘高被2除。这种简洁的表示方法对于把字母固定成数的希腊人来说是根本不能使用的。
后来,罗马人打败了希腊人,成为地中海地区的霸主。他们在希腊人的基础上,建立了自己的记数方法。大约两千年前,罗马军队征服了欧洲南部、高卢、英国大部分、非洲北部边缘和西亚的大片地区。希腊语作为学习的语言被保留下来。
公元四世纪,罗马帝国分为东西两个部分。东罗马部分继承了希腊文明,保存了希腊的学术语言和传统;而西罗马就很快丢掉了希腊的语言和科学,长期处于落后保守之中,停步不前。
西方在数学、科学等各个方面需要学习和援助。这些援助来自东方的阿拉伯、印度和中国。






