|
|
 |
专题栏目 |
 |
|
相关文章 |
|
|
|
|
|
 |
[组图]椭球体积公式的中学证法 |
热 ★★★ |
|
椭球体积公式的中学证法
|
|
作者：未知 文章来源：别处引用 点击数： 更新时间：2006/3/5 23:46:03  |
|
高中课本给出了圆球体积公式的证明过程，而椭球的体积公式是如何证明的呢？其实我们完全可以运用中学所学的知识来证明椭球的体积公式。下面的证明借鉴了高中课本中证明圆球体积公式的方法，但愿证明方法二也能引入到高中的课本中去。
证明方法一：
[注：此证明方法是刚读高一时，在没有学习到椭圆方程等的情况下作出的。此证明方法利用到了物理学中的液体压强公式 P=ρgh 及压强的定义式 P=F/S 。椭球体积公式的导出，起因于读初中时对液体压强公式的怀疑。此证明方法在此暂不给出。]
证明方法二：
如图（1），将底面直径皆为2b，高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上。以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面。有
S圆 =π(m2-d2) 【1】
S环 =πb2-πr2=π(b2-r2)
因为 r/b=d/a（三角形相似）
所以 S环 =π(b2-b2d2/a2) 【2】
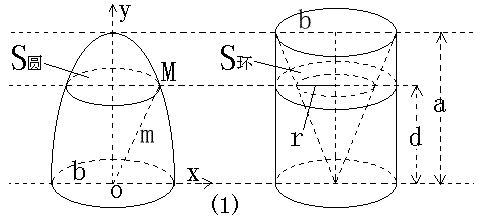
将M点的坐标值代入椭圆方程x2/b2+y2/a2=1中有
(m2-d2)/b2+d2/a2=1
即 m2-d2=b2-b2d2/a2 【3】
将【1】、【2】代入【3】得
S圆=S环
再根据祖恒原理可知，这两个几何体是相等的。
即 V椭/2=V柱-V锥=πab2-πab2/3
即 V椭=4πab2/3
当椭半球体的截面不是圆面而是椭圆面时,我们可推导得到椭球的体积公式为4πabc/3 。
下面的证明得到了新华网论坛昵称为 瞎话瞎说 wdzg168 等网友的帮助。特此致谢！〖点击阅读〗
如图（2），将底面积皆为πbc，高皆为a的椭半球体及已被挖去了椭圆锥体的椭圆柱体放置于同一平面β上。以平行于平面β的平面于距平面β任意高d处可横截得到S椭及S环两截面。
将M点的坐标值代入椭球面方程x2/b2+y2/a2+z2/c2=1中有
(m2-d2)/b2+d2/a2=1
即 m2-d2=b2-b2d2/a2 【A】
将N点的坐标值代入椭球面方程x2/b2+y2/a2+z2/c2=1中有
d2/a2+(n2-d2)/c2=1
即 n2-d2=c2-c2d2/a2 【B】
将【A】、【B】代入S椭的公式
S2椭 =π2(m2-d2)(n2-d2)中得到
S2椭/π2 =b2c2+b2c2d4/a4-2b2c2d2/a2 【C】
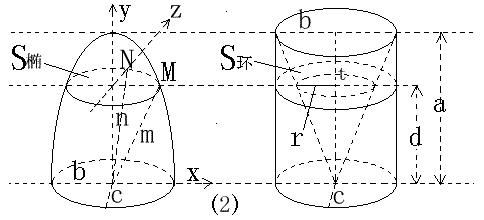
S环 =πbc-πrt=π(bc-rt)
即 S2环/π2 =(bc-rt)2 =b2c2+r2t2-2bcrt
因为 r/b=d/a,t/c=d/a（三角形相似）
所以 S2环/π2 =b2c2+b2c2d4/a4-2b2c2d2/a2 【D】
据【C】、【D】可知
S椭 = S环
再根据祖恒原理可知，这两个几何体是相等的。
即 V椭/2=V柱-V锥=πabc-πabc/3
即 V椭=4πabc/3
|
|
| 学术科研录入：admin 责任编辑：admin |
|
|
上一个学术科研： 对新编高中数学教材中球面积、球体积公式处理方案的考虑
下一个学术科研： 中小学数学教育该怎样引导? |
|
|
| 【字体：小 大】【发表评论】【加入收藏】【告诉好友】【打印此文】【关闭窗口】 |
|
 网友评论：（只显示最新10条。评论内容只代表网友观点，与本站立场无关！） |
| |
|
|
|
|
